Here’s the Link to Part 1.

   

I am currently staying at Udaipur, a lake city in Rajasthan, India. Working with a view like this will be so accessible; I had never thought, and it is so much fun. Perks of the post-covid world. Although, I am not entirely sure whether we can call it post-covid certainly yet given the headlines in China today.

Elegant numbers

Prime numbers have a certain elegance and simplicity about them. They are the building blocks of the natural numbers, and have played a central role in the development of mathematics.

A prime number is a positive integer greater than 1 that is not a product of two smaller integers. For example, the first few prime numbers are 2, 3, 5, 7, 11, and 13.

One of the most interesting properties of prime numbers is that they are relatively rare, which makes them hard to predict and find.

This has led to the development of many different algorithms and techniques for identifying prime numbers, and has also made them the subject of much study in mathematics and computer science.

Are Prime Numbers Beautiful?

I agree, prime numbers are beautiful! They are simple, yet fundamental to the structure of the natural numbers. One of the most interesting properties of prime numbers is that they are relatively rare, which makes them hard to predict and find. This has led to the development of many different algorithms and techniques for identifying prime numbers, and has also made them the subject of much study in mathematics and computer science. Prime numbers have many interesting properties and have played a central role in the development of mathematics and the study of number theory.

Many famous problems and theorems in mathematics are related to prime numbers, and they continue to fascinate mathematicians and scientists to this day.

Divisibility

For a number x to divide a number y, all primes in x’s prime factorisation must be present in y’s prime factorisation. This can also be written as following -

Given mod(y,x)=0, and

x = 2^j0 * 3^j1 * 5^j2 * 7^j3 * 11^j4 * ...
y = 2^k0 * 3^k1 * 5^k2 * 7^k3 * 11^k4 * ...

Then for all i, ji <= ki.

I hope you are still with me :laughing:

Using above conjecture, one can arrive at the following, we will probably discuss the proof later -

xy = gcd(x,y) * lcm(x,y)

Here’s the link to a program that does the exact same thing. You can try it yourself by running clj -M prime.clj in your local. Following screenshots showcase that both pairs of multiplication, i.e x*y, and gcd*lcm are equal.
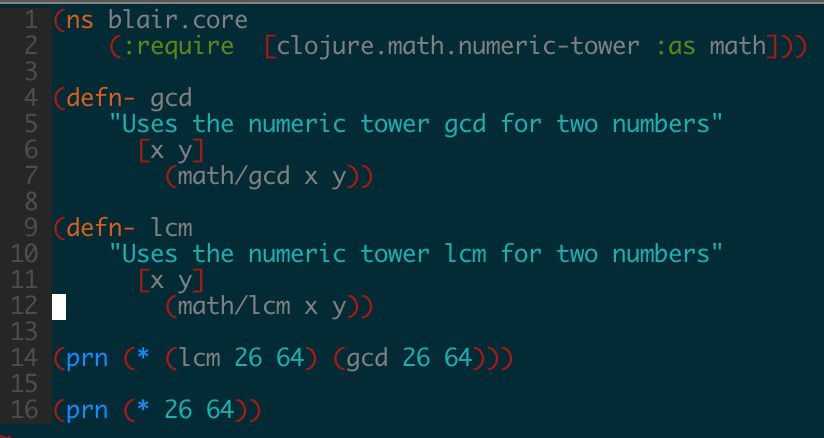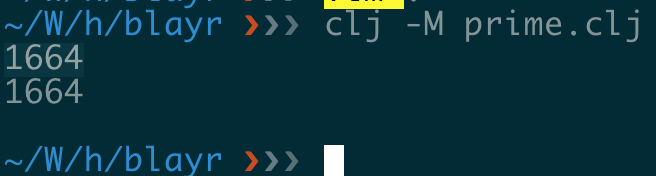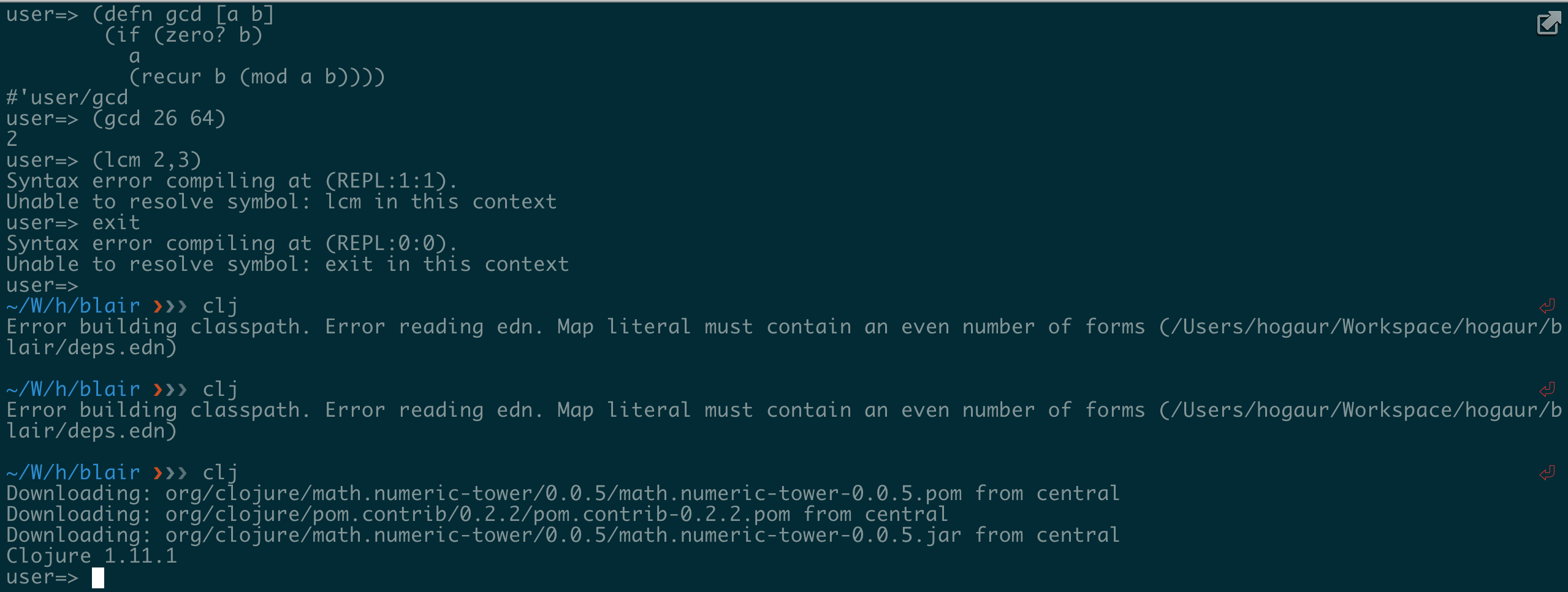Notice how I navigated the deep realms of the repl :laughing: :laughing:

Conclusion

I decide to go through the backlog and get something done. It is not essential to put a date on every project, if you show some respect to your backlog. I decidedly to try out ChatGPT today and publish a blog. Guess what, this blog is mostly written automatically using OpenAI. Of course, some part of it is original, of course.

If you want to cafe hop in Udaipur, go to Gangour Ghat Marg. I spent most of my time here at Savage Garden.

Keep it charged :thumbsup:

Cheers :beers: